frontend-notes
浮点数精度
十进制 => 二进制
你以十进制的数除以你所要转换的进制数,把每次除得的余数记在旁边,所得的商数继续除以进制数,直到余数为0时止.例如你要把101转换成二进制:
101/2=50...(余数为1);
50/2=25....(余数为0);
25/2=12....(余数为1);
12/2=6.....(余数为0);
6/2=3......(余数为0);
3/2=1......(余数为1);
1/2=0......(余数为1);
然后把相应的余数从低向高顺着写出来,如上的为1100101,此即为100的二进制表示形式.
即 100 = 1 * 2^6 + 1 * 2^5 + 0 * 2^4 + 0 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0
上面说的是整数的转换方法,那么小数怎么办呢 同理,如果要转换0.75,则转换方法如下
0.75 = a * 2^-1 + b * 2^-2 + c * 2^-3 + d * 2^-4...
// 因为使用的是二进制,这里的 abcd……的值的要么是 0 要么是 1。
// 那怎么算出 abcd…… 的值呢,我们可以两边不停的乘以 2 算出来,解法如下:
// 两边同时乘以2
1 + 0.5 = a * 2^0 + b * 2^-1 + c * 2^-2 + d * 2^-3... (所以 a = 1)
// 剩下的:
0.5 = b * 2^-1 + c * 2^-2 + d * 2^-3...
// 再同时乘以 2
1 + 0 = b * 2^0 + c * 2^-2 + d * 2^-3... (所以 b = 1)
所以 0.75 用二进制表示就是 0.ab,也就是 0.11
如果用以上方法计算0.1,得到的将是一个不停循环的数0.00011001100110011……
js浮点数存储
那么js是如何这些存储浮点数的呢?
ECMAScript 使用 64 位来储存一个浮点数,并且存储方式遵循 IEEE754标准
Value = sign * exponent * fraction
看起来很抽象的样子,简单理解就是科学计数法…… 比如 -1020,用科学计数法表示就是:
-1 * 10^3 * 1.02
其中sign 就是 -1,exponent 就是 10^3,fraction 就是 1.02
对于二进制也是一样,以 0.1 的二进制 0.00011001100110011…… 这个数可以表示为
1 * 2^-4 * 1.1001100110011……
其中 sign 就是 1,exponent 就是 2^-4,fraction 就是 1.1001100110011……
把这个公式在转变一下:
V = (-1)^S * (1 + Fraction) * 2^E
- S:S表示符号位,当 S = 0,V 为正数;当 S = 1,V 为负数。
- Fraction:再看 (1 + Fraction),这是因为所有的浮点数都可以表示为 1.xxxx * 2^xxx 的形式,前面的一定是 1.xxx,那干脆我们就不存储这个 1 了,直接存后面的 xxxxx 好了,这也就是 Fraction 的部分
- E:如果是
1020.75,对应的二进制为1111111100.11,E值为9;如果是0.1,对应的二进制为0.00011001100110011……,E值为-4。E 既可能是负数,又可能是正数,那问题就来了,那我们该怎么储存这个 E 呢?- 假如我们用 8 位来存储 E 这个数,如果只有正数的话,储存的值的范围是 0 ~ 254,而如果要储存正负数的话,值的范围就是 -127~127,我们在存储的时候,把要存储的数字加上 127,这样当我们存 -127 的时候,我们存 0,当存 127 的时候,存 254,这样就解决了存负数的问题。对应的,当取值的时候,我们再减去 127。
- 所以呢,真到实际存储的时候,我们并不会直接存储 E,而是会存储 E + bias,当用 8 位的时候,这个 bias 就是 127。
所以,如果要存储一个浮点数,我们存 S 和 Fraction 和 E + bias 这三个值就好了,那具体要分配多少个位来存储这些数呢?IEEE754 给出了标准:
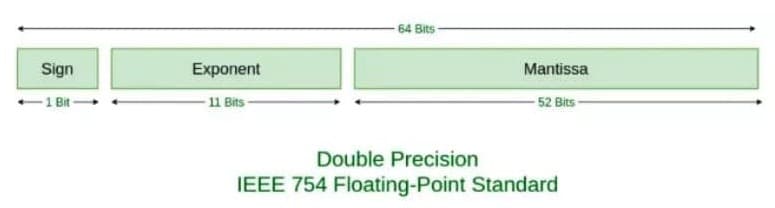
- 我们会用 1 位存储 S,0 表示正数,1 表示负数。
- 用 11 位存储 E + bias,对于 11 位来说,bias 的值是 2^(11-1) - 1,也就是 1023。
- 用 52 位存储 Fraction。
例如:0.1对应二进制是 1 * 1.1001100110011…… * 2^-4,则Sign 是 0,E + bias 是 -4 + 1023 = 1019,1019 用二进制表示是 1111111011,Fraction 是 1001100110011……
对应 64 位的完整表示就是:
0 01111111011 1001100110011001100110011001100110011001100110011010
同理, 0.2 表示的完整表示是
0 01111111100 1001100110011001100110011001100110011001100110011010
所以当 0.1 存下来的时候,就已经发生了精度丢失,当我们用浮点数进行运算的时候,使用的其实是精度丢失后的数。
浮点数的运算
关于浮点数的运算,一般由以下五个步骤完成:对阶、尾数运算、规格化、舍入处理、溢出判断。我们来简单看一下 0.1 和 0.2 的计算。
首先是对阶,所谓对阶,就是把阶码调整为相同,比如 0.1 是 1.1001100110011…… * 2^-4,阶码是 -4,而 0.2 就是 1.10011001100110…* 2^-3,阶码是 -3,两个阶码不同,所以先调整为相同的阶码再进行计算,调整原则是小阶对大阶,也就是 0.1 的 -4 调整为 -3,对应变成 0.11001100110011…… * 2^-3
接下来是尾数计算:
0.1100110011001100110011001100110011001100110011001101
+ 1.1001100110011001100110011001100110011001100110011010
————————————————————————————————————————————————————————
10.0110011001100110011001100110011001100110011001100111
得到的结果为:10.0110011001100110011001100110011001100110011001100111 * 2^-3
格式化变成:1.0011001100110011001100110011001100110011001100110011(1) * 2^-2
括号里的 1 意思是说计算后这个 1 超出了范围,所以要被舍弃了。
再然后是舍入,四舍五入对应到二进制中,就是 0 舍 1 入,因为我们要把括号里的 1 丢了,所以这里会进一,结果变成1.0011001100110011001100110011001100110011001100110100 * 2^-2
本来还有一个溢出判断,因为这里不涉及,就不讲了。
所以最终的结果存成 64 位就是
0 01111111101 0011001100110011001100110011001100110011001100110100
将它转换为10进制数就得到 0.30000000000000004440892098500626
因为两次存储时的精度丢失加上一次运算时的精度丢失,最终导致了 0.1 + 0.2 !== 0.3
其他
// 十进制转二进制
parseFloat(0.1).toString(2);
=> "0.0001100110011001100110011001100110011001100110011001101"
// 二进制转十进制
parseInt(1100100,2)
=> 100
// 以指定的精度返回该数值对象的字符串表示
(0.1 + 0.2).toPrecision(21)
=> "0.300000000000000044409"
(0.3).toPrecision(21)
=> "0.299999999999999988898"